Внешние нагрузки определяются переменными гидрометеорологическими условиями района плавания судов. В разное время года температура наружного воздуха может изменяться от +45 °С до -50 °С. Влагосодержание в 1 кг воздуха изменяется от 24…26 до 0,1…0,5 г. Температура наружного воздуха, непрерывно изменяясь, претерпевает сезонные, суточные, а также более короткие по продолжительности колебания. В условиях переменных тепловлажностных нагрузок существенно изменяется интенсивность солнечной радиации. В результате облучаемая поверхность нагревается сильнее, чем окружающий воздух. Величина нагрева поверхности зависит от времени года и суток, ориентации судовых ограждений по сторонам света, географической широты, состояния атмосферы. Если учесть, что суда представляют большие металлические сооружения с высокой теплопроводностью, то становится ясно, насколько велико влияние внешних условий на формирование микроклимата в обитаемых помещениях судов.
К внутренним нагрузкам относятся тепловлажностные выделения оборудования и людей. При этом помимо температуры и относительной влажности воздуха его подвижность в помещении также оказывает тепловое воздействие на человека. Известно, что подвижность воздуха усиливает конвекцию и ускоряет испарения с поверхности кожи человека.
Для описания статических и динамических характеристиккондиционируемого помещения применяют методы, использующие уравнения тепловлажностного баланса на основе средних значений входных и выходных параметров. Динамические характеристики кондиционируемого помещения обычно описываются с помощью дифференциальных уравнений в частных производных с допущениями, что по всему объему помещения происходит достаточно хорошее перемешивание воздуха, а само помещение рассматривается как объект с сосредоточенными параметрами.
Подобный подход оправдан стремлением привести математическую модель рассматриваемого звена системы автоматического управления (САУ) к виду, пригодному для дальнейших исследований системы комфортного кондиционирования воздуха (СККВ) в целом. Следует учитывать, что математическая модель обслуживаемого помещения разрабатывается в целях дальнейшего анализа САУ, а не для исследования, например, воздушного режима в нем. Анализ литературных источников показал, что существующие динамические модели кондиционируемого помещения обладают большим числом исходных упрощений, что ограничивает области использования таких моделей при разработке САУ СККВ. В частности, не учитывается подвижность воздуха в помещении, а также способ его подачи через воздухораспределитель.
При разработке достоверной модели кондиционируемого помещения как многопараметрического объекта регулирования необходимо выявить максимально необходимое для создания САУ число внутренних связей объекта. В первую очередь следует определить количественные характеристики, связывающие температуру, относительную влажность и подвижность воздуха, а также выявить основные параметры помещения, характеризующие его в переходных процессах. Кроме того, при разработке САУ необходимо исследование нестационарных тепловлажностных процессов в кондиционируемом помещении. Учет нестационарного характера внешних и внутренних тепловлажностных нагрузок на кондиционируемое помещение позволяет синтезировать энергоэффективную САУ СККВ.
Разрабатываемая модель кондиционируемого помещения судна как объекта регулирования по температуре и относительной влажности должна описывать прежде всего связи параметров по каналам: температура приточного воздуха (ТП) — температура воздуха в помещении (ТУ); относительная влажность приточного воздуха (ϕП) — относительная влажность воздуха в помещении (ϕУ). При выводе управления модели, описывающего динамические свойства помещения по каналу температура приточного воздуха — температура воздуха в помещении использовалось уравнение теплового баланса для помещения в условиях хорошего перемешивания воздуха. Само помещение рассматривалось как объект с сосредоточенными параметрами.
Исходное уравнение теплового баланса для помещения имеет вид:
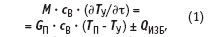
где QИЗБ — общие теплоизбытки в помещении;
M — масса воздуха в помещении;
GП — расход приточного воздуха;
cB — удельная теплоемкость воздуха.
Общие теплоизбытки QИЗБ в уравнении (1) определяются следующим образом по формуле:
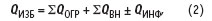
где QОГР — суммарные теплопритоки через наружные ограждения:
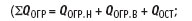
QОГР.Н , QОГР.В — тепловые потоки через изолированные наружные и внутренние поверхности ограждений помещения;
QОСТ — тепловой поток через иллюминаторы);
QВН — суммарные внутренние теплопритоки:
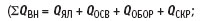
QЯЛ — теплопритоки от людей с учетом их физической деятельности;
QОСВ — теплопритоки от освещения;
QОБОР — теплопритоки от оборудования;
QСКР — скрытые теплопритоки);
QИНФ — тепло, вносимое воздухом при инфильтрации.
После соответствующих подстановок в уравнение (1) компонентов QИЗБ, а также конструктивных и теплотехнических характеристик помещения (при малых отношениях измененных параметров) уравнение переходного процесса с использованием преобразования Лапласа имеет следующий вид:
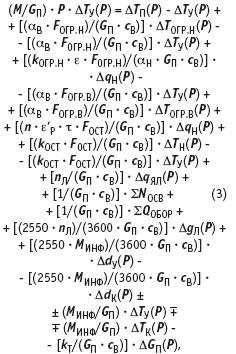
где n — число иллюминаторов в каюте;
nЛ — число человек в каюте;
, ’P — коэффициенты поглощения наружным ограждением и остеклением;
— коэффициент пропускания солнечной радиации;
NОСВ, QОБОР — мощность источников освещения и оборудования;
qЯЛ, gЛ — тепло и влаговыделения одним человеком;
М — масса воздуха в помещении;
MИНФ — масса воздуха, проникающая в кондиционируемое помещение при открывании двери и через щели.
Уравнение (3), пригодное для реализации динамической модели помещения, после соответствующих преобразований имеет следующий вид:
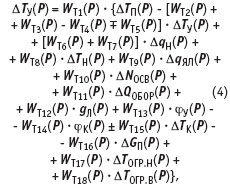
где WT1...WT18(P) — передаточные функции, параметры которых приведены в
таблице.
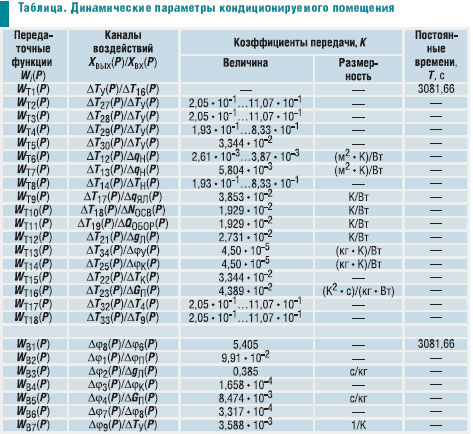
В
таблице переменные параметры передаточных функций WT2(P), WT3(P), WT4(P), WT6(P), WT8(P), WT17(P) и
WT18(P) определяются в зависимости от изменяющейся величины подвижности воздуха в помещении и способа его подачи в помещение.
При выводе уравнения модели, описывающего динамические свойства помещения по каналу, относительная влажность приточного воздуха — относительная влажность воздуха в помещении использовалось уравнение материального баланса (баланса влаги) в помещении:
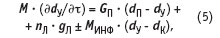
где dП, dУ, dK — влагосодержание приточного воздуха, воздуха в помещении и инфильтрующего воздуха соответственно.
Используя преобразование Лапласа, уравнение (4) было приведено к следующему виду:
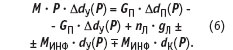
Уравнение (5) после соответствующих преобразований имеет следующий вид:
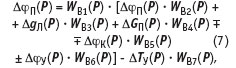
где WВ1(P)…WВ7(P) — передаточные функции.
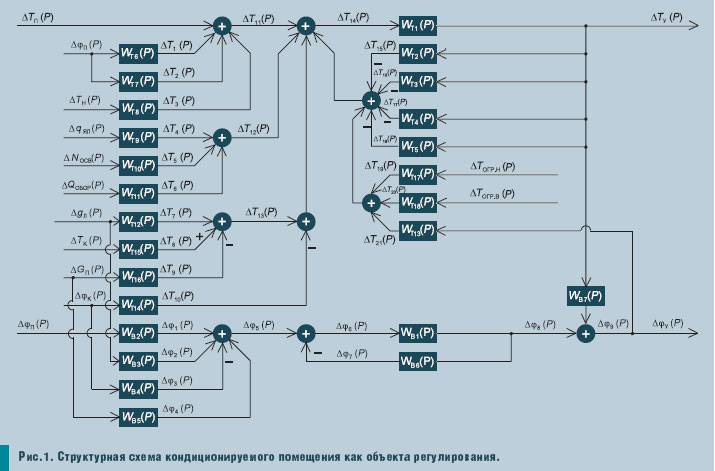
Полученные уравнения (4) и (7) являются уравнениями математической модели кондиционируемого помещения судна как объекта регулирования. Разработанная структурная схема кондиционируемого помещения как объекта регулирования по температуре и относительной влажности воздуха приведена на
рис. 1. На основе уравнений (4) и (7) была разработана модель помещения, пригодная для исследования его динамических свойств в MATLAB 6.5 — Simulink.
Результаты моделирования помещения в Simulink при ступенчатом характере возмущающих воздействий по каналам ТП — ТУ и ϕП — ϕУ для скоростей воздуха в помещении B = 1–0,1 м/с…5–0,5 м/с при отрывных струях подаваемого воздуха через воздухораспределитель приведены на рис. 2 и 3. При моделировании использовались коэффициенты передачи и постоянные времени соответствующих передаточных функций, значения которых приведены в таблице. Полученные характеристики отражают переходной процесс в помещении при изменениях параметров ТП и ϕП.
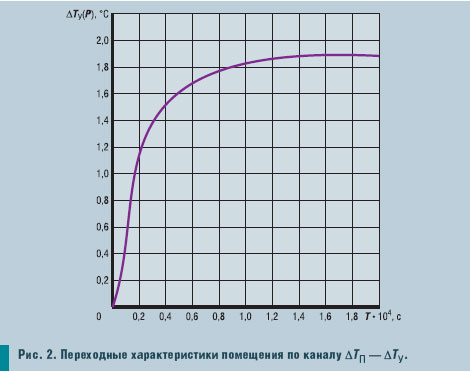
Анализ результатов исследования показал, что математическое описание и полученные на его основе кривые переходных процессов по каналам ТП — ТУ и ϕП — ϕУ с достаточной для проектирования САУ точностью отражают реальные процессы, происходящие в кондиционируемом помещении судна. Это позволяет использовать модель кондиционируемого помещения для разработки САУ СККВ при нестационарных тепловлажностных нагрузках, что позволит обеспечить комфортный микроклимат воздушной среды в каютах согласно действующим нормативным положениям.









