В данной статье представлен расчет процессов автоматического регулирования системы кондиционирования воздуха для помещения с постоянными теплопоступлениями на примере фабрики по выращиванию грибов.

При проектировании автоматизированных систем вентиляции и кондиционирования воздуха (СВ и КВ) основной особенностью является необходимость расчета нестационарного теплового режима обслуживаемого помещения с учетом автоматического регулирования СВ и КВ и переходных процессов в их обо-рудовании, связанных с изменением параметров наружного и внутреннего воздуха с течением времени.

Основой предлагаемой методики является предположение, что общая теплоустойчивость системы «помещение- СВиКВ-САР» складывается из показателя теплопоглощения помещения и управляющего воздействия системы автоматического регулирования (САР). Это непосредственно следует из встречно-параллельного включения звеньев, соответствующих помещению и СВ и КВ в схеме автоматического управления внутренним микроклиматом (рис. 1) [1].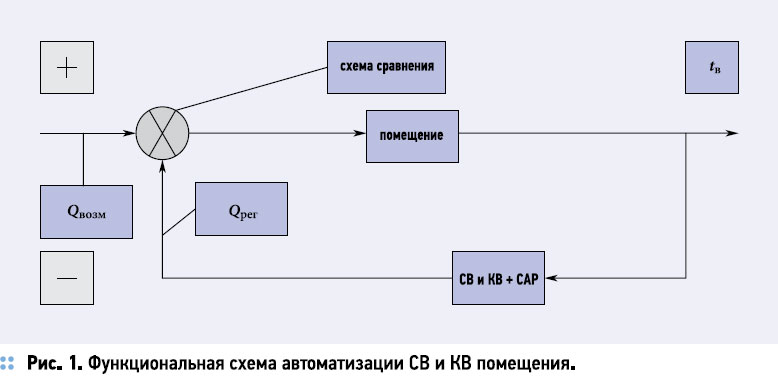

Можно показать, что в рассматриваемых условиях поддержание tB = const физически невозможно, хотя бы из-за наличия существенной зоны нечувстви-тельности и их инерционности у датчиков температуры, входящих в САР, а, главное, вследствие тепловой инерции ограждений помещения. Поэтому нужно задаться максимальным отклонением tB от уставку (AtB max).

При этом сама СВ и КВ и ее САР образуют для рассматриваемого помещения отрицательную обратную связь по каналу «теплопоступления Qвозм - tв», поскольку входной информацией для их работы является величина отклонения tв от заданного среднего уровня, а результатом их действия - тепловой ПОТОК Qрег, который добавляется к Qвозм, полностью или частично компенсируя его и внося, таким образом, дополнительное стабилизирующее воздействие в систему «помещение-СВиКВ-САР».

В нашем случае колебания теплопоступлений от внутренних источников в помещении практически отсутствуют (технологические тепловыделения от грибов, освещения и т.д. примерно постоянны), поэтому роль Qвозм играют отклонения, связанные с изменением температуры наружного воздуха tн, передающиеся через приточную установку в помещение.

Именно их и должна при этом компенсировать САР.

Построим математическую модель процессов в трехмодульной системе «помещение-СВиКВ-САР», учитывающую, в отличие от существующих [2, 3], нелинейность помещения как объекта регулирования при однократном тепловом воздействии за счет сочетания элементов классической теории автоматического управления (ТАУ) и теории теплоустойчивости.

Предполагаем, что регулирование воздухонагревателя осуществляется по ка чественной схеме, с применением трехходового клапана на перемычке и, соот-ветственно, с изменением температуры нагретой воды на входе в аппарат в зависимости от текущей потребности в нагревании воздуха.

Тогда математическая модель процессов в воздухонагревателе СВ и КВ, управляемом САР и в обслуживаемом помещении может быть представлена следующей системой уравнений [4]: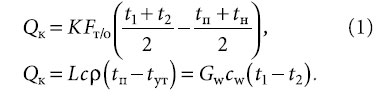

где Fто — поверхность теплообмена воздухонагревателя, м2; Qк — его тепловая мощность, Вт; Gw, — массовый расход теплоносителя, т.е., в данном случае, нагретой воды, кг/с; cw, — ее удельная теплоемкость, равная 4190 Дж/(кг-К); L, c и p — объемный расход приточного воздуха [м3/с], его удельная теплоемкость — 1005 Дж/(кг-К) и плотность, принимаемая в размере 1,2 кг/м3, соответственно; К — коэффициент теплопередачи теплообменника, Вт/(м2-К).

Параметры t1 и t2 представляют собой температуру воды, соответственно, на входе и на выходе из теплообменника, °С; tп и tн — температура приточного воздуха, поступающего в помещение после нагрева в аппарате, и его же температура до подогрева (после теплоутилизатора или, при его отсутствии — наружная).
Тогда tср — средняя температура воды в воздухонагревателе:

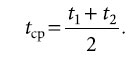
Отсюда после некоторых преобразований получаем: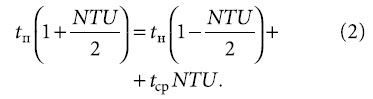

Здесь безразмерный комплекс:

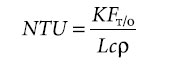
представляет собой число единиц переноса теплоты для воздуха в воздухонагревателе [4].

В данном случае: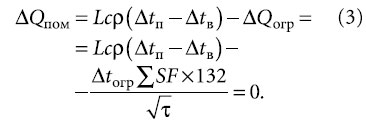

по результатам подбора приточной установки типа КЦКП производства компании ООО «ВЕЗА» с помощью компьютерной программы [5].

Для обслуживаемого помещения уравнение мгновенного теплового баланса, если пренебречь теплоаккумуляционной способностью объема внутреннего воздуха, можно записать в следующем виде [2]: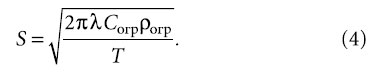

Здесь ΔQогр — отклонение от среднего значения величины теплового потока, проходящего через внутреннюю поверхность ограждающих конструкций помещения, Вт; Δtп и Δtв — отклонения tп и tв от расчетных значений. Величину ΔQогр можно определить через характеристики слоя материала конструкций, захватываемого температурной волной, начинающей распространяться с момента температурного возмущения, вызванного изменением tн. Именно от этого момента мы и отсчитываем время τ. Параметр F — площадь поверхностей ограждений, обращенных в помещение. Для рассматриваемого объекта ее значение равно 680 м2.

Величина S является комплексной теплофизической характеристикой материала — т.е., в данном случае, его коэффициентом теплоусвоения [2]: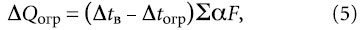

где T — период колебаний, для которого рассчитывается величина S (обычно 24 ч, т.е. 86400 с); λ представляет собой теплопроводность материала ограждений, обращенного в помещение, Вт/(м-К); c_огр и ρ_огр — удельная теплоемкость [Дж/ (кг*К)] и плотность [кг/м3] материала, соответственно. Для применяемого материала (керамзитобетон характеризуется рогр = 1600 кг/м3) S = 10,77 Вт/(м2-К) [6]. Выражение (3) может быть получено на основе сочетания элементов теории теплоустойчивости и уравнения для распространения температурной волны при однократном тепловом воздействии [2].

Одновременно можно записать выражение для ΔQ_orp через интенсивность теплообмена между воздухом помещения и поверхностями ограждений:

где α — коэффициент общего теплообмена на поверхностях, его значение можно принять равным =6,25 Вт/(м К) [7].

Поскольку характерная продолжительность теплового возмущения и соответствующее время регулирования в условиях данной рассматриваемой задачи составляют сотни и тысячи секунд, что во много раз превышает постоянные времени таких элементов системы, как датчики САР и теплообменное оборудование, инерционностью данных устройств вполне можно пренебречь и полностью считать их линейными пропорциональными звеньями. В то же время нелинейность и инерционность помещения как объекта регулирования учитывается непосредственно уравнением (3).

Поэтому для отрицательной обратной связи, входящей в схему управления тепловым режимом помещения (рис. 1), если считать в первом приближении, что t₂ = const, т.е. за счет работы САР меняется только величина t₁, можно легко записать следующее равенство:

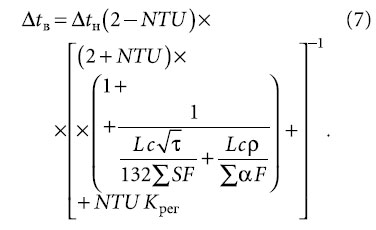
где Δt₁ представляет собой отклонение t₁ от исходного уровня.

Уравнение (6) замыкает систему (2-5). В данном случае по своему физическому смыслу коэффициент передачи K_рег показывает, на сколько градусов нужно изменять температуру нагретой воды на входе в калорифер при отклонении t_в от уставки на 1 К. Такое изменение и должна обеспечить соответствующим образом подобранная САР. При записи (6) был принят П-закон регулирования, т.е., фактически, выделена пропорциональная часть в управляющем воздействии, т.к. Д-компонентой можно пренебречь из-за значительного временного интервала, а И-составляющая будет уводить закон регулирования от оптимального, вступая в противоречие с теплоинерционными свойствами помещения [8].

В системе (2-6) неизвестными являются Δt_п, Δt_в, Δt_огр. Величину Δt_н считаем заданной и равной 3,25 °С по данным [9], т.е. половине суточной амплитуды колебаний наружной температуры в холодный период года для города Москвы. После ряда преобразований получаем формулу для основной интересующей нас величины Δt_в: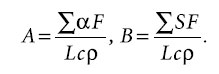

Введем еще безразмерные параметры:

По аналогии с NTU их можно назвать числом единиц переноса теплоты для внутренних поверхностей ограждений помещения и для материального слоя, в пределах которого распространяется температурная волна. В условиях рассматриваемого примера после подстановки числовых значений находим: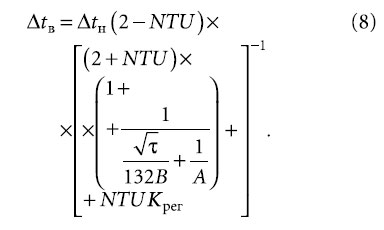

Тогда выражение для текущего отклонения температуры внутреннего воздуха от уставки будет иметь вид:

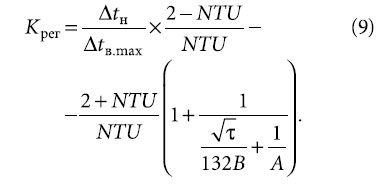
Отсюда для требуемого коэффициента передачи регулятора из условия ограничения величины Δt_в, получаем:

Если перед калорифером установлен теплоутилизатор, в формулу (9) вместо Δt_н необходимо подставлять величину

Δt_н= Δt_н (1-K_эф),
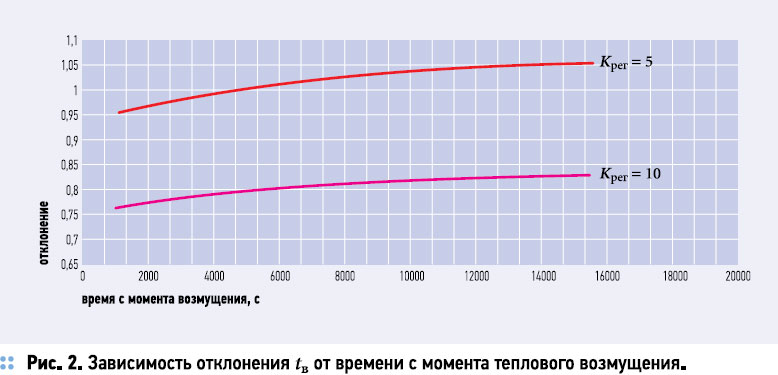
где К_эф — коэффициент температурной эффективности теплоутилизационного оборудования.

Зависимость изменения Δt_в от т при значениях К_рег = 5 (верхняя линия) и 10 (нижняя линия) приведены на рис. 2. Легко видеть, что с течением времени отклонение температуры в помещении постепенно растет, но скорость этого увеличения замедляется из-за ассимиляции теплового возмущения внутренним слоем ограждающих конструкций. При этом с ростом Крет отклонение также становится меньше из-за усиления регулирующего воздействия.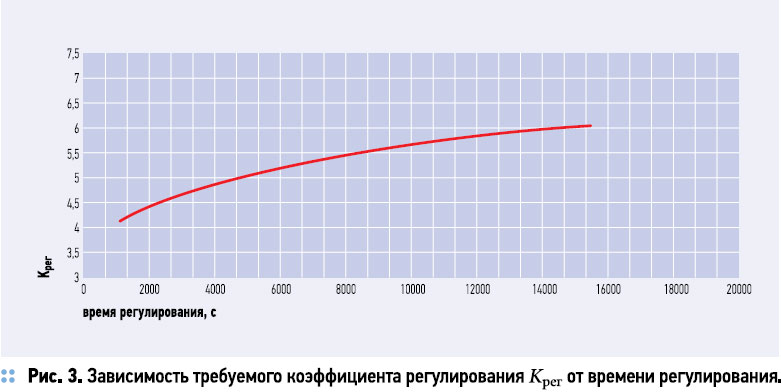

Зависимость требуемого значения К_рег от времени регулирования при величине Δt_в.max = 1 °С показана на рис. 3. Таким образом, чем более продолжителен временной интервал, в течение которого нам нужно поддерживать температуру в помещении на заданном уровне, тем более интенсивное воздействие со стороны САР оказывается необходимым. Однако зависимость эта довольно слабая. В среднем в данном случае требуется величина К_рег около 5, т.е. на каждый градус отклонения t_в от уставки необходимо изменять температуру воды на входе в воздухонагреватель примерно на 5 °С, и САР должна обеспечить такое воздействие.

Итак, мы получили методику, позволяющую оценить влияние отклонений температуры наружного воздуха на внутреннюю температуру в помещении с постоянными теплопотерями и тепло- поступлениями, обслуживаемом автоматизированной системой СВ и КВ, с учетом его теплоинерционности и характеристик вентиляционного оборудования и САР, а также определять требуемый коэффициент передачи регулятора в зависимости от времени регулирования и допустимого отклонения внутренней температуры. Методика имеет достаточно простой и инженерный вид и доступна для использования на этапе предварительных расчетов и принятия основных решений по устройству СВ и КВ.

1. Самарин О.Д. Теплофизика. Энергосбережение. Энергоэффективность. — М.: АСВ,2009.
3. Калмаков A.A. и др. Автоматика и автоматизация систем теплогаз о снабжения и вентиляции. — М.: Стройиздат, 1986.
4. Теория тепломассообмена. Под ред. А.И. Леонтьева. — М.: Изд-во МГТУ, 1997.
5. Интернет-сайт компании «ВЕЗА» www.veza.ru.
6. СП 23101-2004. Проектирование тепловой защиты зданий. — М.: ГУП ЦПП, 2004.
7. Ананьев А.И., Иванов Л.В., Комов В.М. Исследование теплообмена наружных кирпичных стен жилых зданий и нормирование теплозащитных качеств // Сб. докл. 5-й конф. РНТОС 26-28 апреля 2000 г.
8. Самарин О.Д. Оптимизация мощности и параметров управления систем кондиционирования микроклимата в условиях переменных нагрузок. Автореферат дисс. к.т.н. — М.: МГСУ, 1999.
9. СНиП 2301-99*. Строительная климатология. — М.: ГУП ЦПП, 2004.

Авторы: О.Д. САМАРИН, к.т.н., доцент; С.С. АЗИВСКАЯ, студентка МГСУ